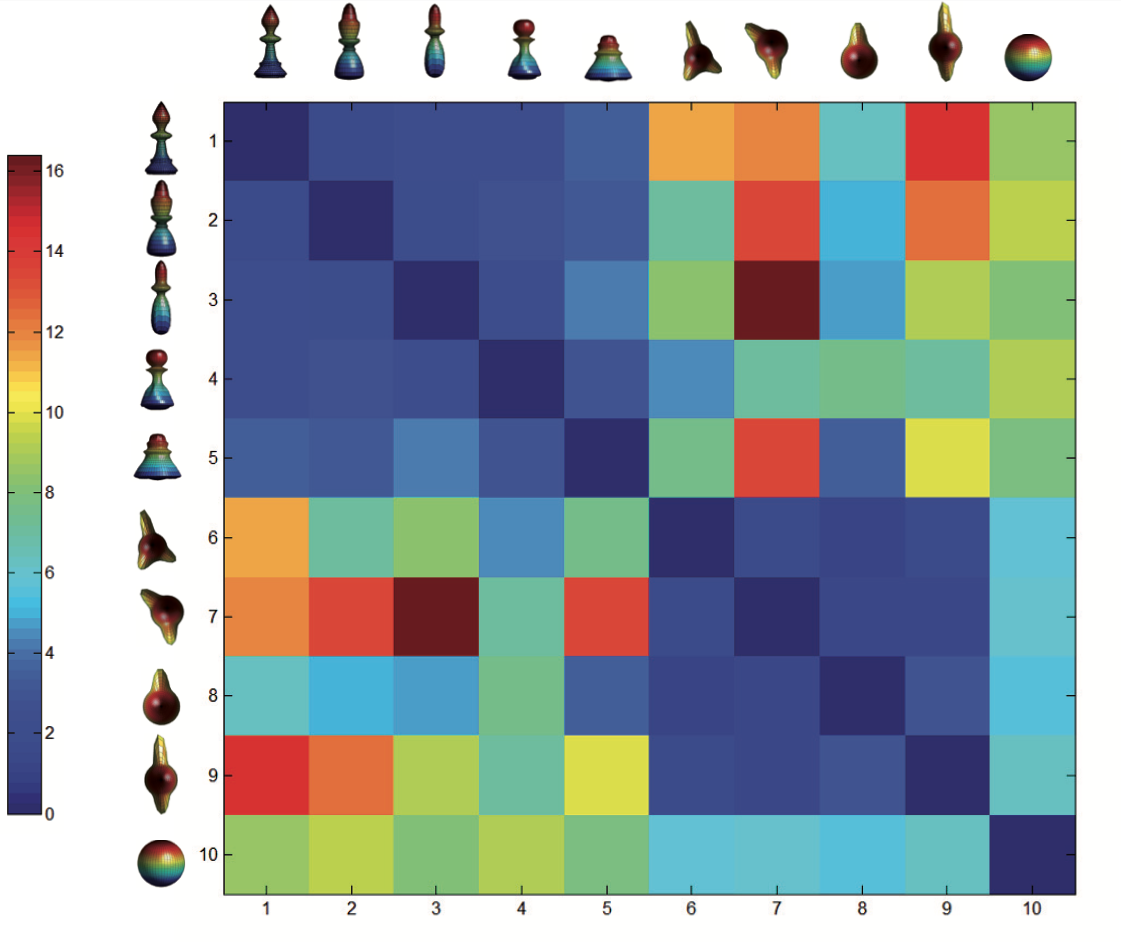
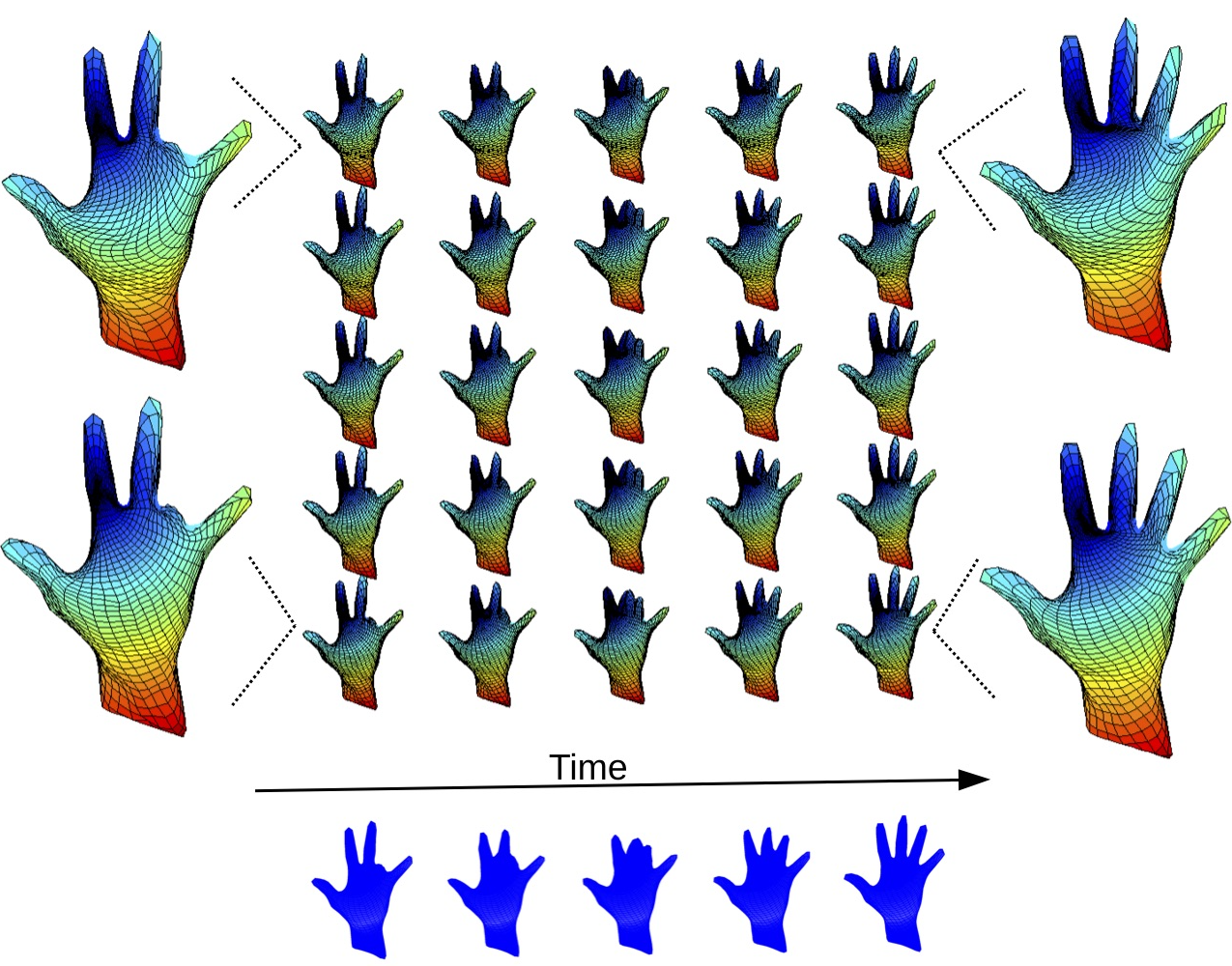
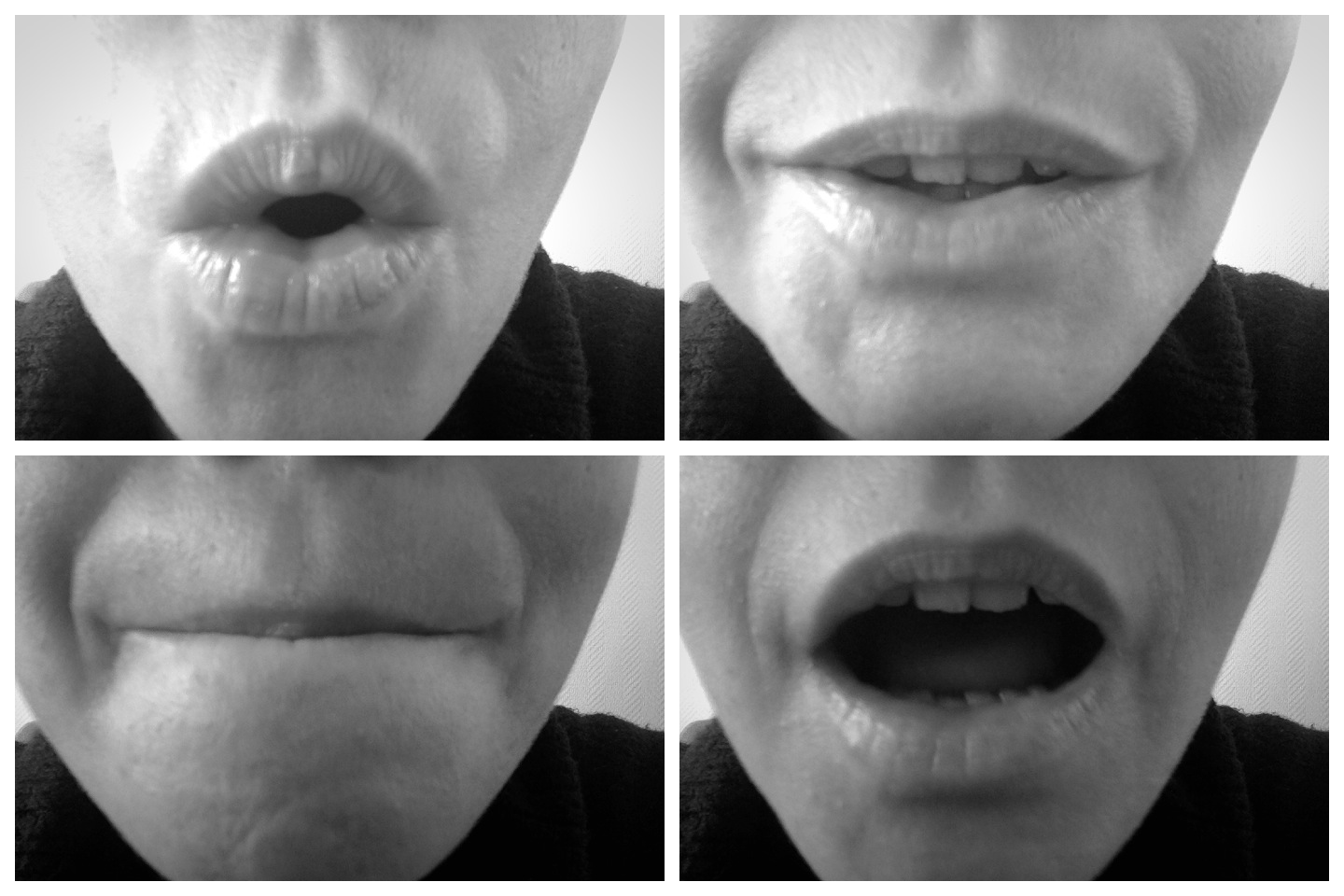
ENS, rue d’Ulm, Paris
The École Normale Supérieure, is a French grande école, and a constituent college of PSL Research University, a collegiate university based in the Latin Quarter of Paris. Among former students of the École Normale Supérieure, one counts 13 Nobel Prizes, 11 Fields Medals, 2 Abel Prizes, 27 Gold Medals of the CNRS Institution, as well as a President and many Ministers and Prime Ministers.
Picture credit: © Ahmed Ben Cheikh

Ecole Polytechnique, Palaiseau, France.
The Ecole Polytechnique is an engineering school under military status, with an important research centre. Among former students, one count the mathematicians Cauchy, Coriolis, Poincaré, Poisson and Mandelbrot, the physicists Becquerel, Carnot, Fresnel, 3 Nobel Prizes, 1 Fields Medals and 3 Presidents.

Paris-Sud University, Orsay, France
Paris-Sud University is probably the best French University for education and research. But aside of its training level, I was attracted by the
large number of sports facilities at the disposal of students : a university swimming pool, a horse-riding centre, 2 professional dance studios, tennis courts, a 300m2 dojo, 2 gyms with the latest weightlifting equipment, many sports halls, and outdoor sports grounds. All this in a green environment not far from Paris…

EPFL, Lausanne, Switzerland
The École polytechnique fédérale de Lausanne (EPFL) is a research institute and university in Lausanne, Switzerland, that specializes in natural sciences and engineering. It is one of the two Swiss Federal Institutes of Technology, and it has three main missions: education, research and technology transfer at the highest international level.
EPFL is widely regarded as a world leading university. The QS World University Rankings ranks EPFL 12th in the world across all fields in their 2017/2018 ranking, whilst Times Higher Education World University Rankings ranks EPFL as the worlds 11th best school for Engineering and Technology.