11h-12h Nathan Ng (Lethbridge)

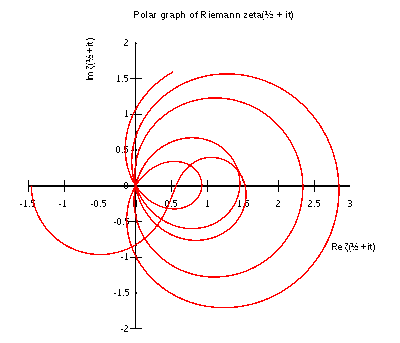
An open question in analytic number theory is: How do the non-trivial zeros of a Dirichlet L-function behave in the critical strip? One might wonder whether the zeros bunch up or if they are well-spaced. In particular, is it possible for the zeros to lie in a vertical arithmetic progression? Let a and b be positive real constants and consider the arithmetic progression {0.5+i(a+kb)} where k ranges between the integers 0 to N. In joint work with Greg Martin, we show that many terms of this arithmetic progression are not zeros of a fixed Dirichlet L-function.

14h-15h Immanuel Halupczok (Münster)

Suppose that X is an affine embedded variety over Z; in other words, we have some polynomials in n variables with integer coefficients and we are interested in the set of zeros. For simplicity, let us assume that there is only a single polynomial f. Fix a prime p and a natural number k, and consider the solutions of f=0 in the ring Z/p^kZ: X( Z/p^kZ) = {(a₁,...,a_n)ε Z/p^kZ : f(a₁,...,a_n) = 0} If we write integers in base p, then each element of X( Z/p^kZ) corresponds to an n-tuple of the last k digits of a₁,...,a_n)ε Z such that the last k digits of f(a₁,...,a_n) are equal to 0. Now, for any tuple (a_i)in X( Z/p^kZ) we can ask how each a_i can be extended by an additional digit to give an element of X( Z/p^k+1Z). Starting with the "tuple of empty numbers" in X( Z/p⁰Z) and adding digits one by one, we get a tree T(X) of possibilities: the nodes of T(X) at distance k from the root (the element of X( Z/p⁰Z) are exactly the elements of X( Z/p^kZ), and each element of X( Z/p^kZ) is connected to the element of X( Z/p^k-1Z) which one obtains by forgetting one digit of every coordinate. The question I want to consider in this talk is: What can one say about the structure of the tree T(X) (for arbitrary )? There is an old result by Meuser and Denef about the rationality of certain Poincaré series which suggests that these trees are far from arbitrary, and this indeed turns out to be true. For p sufficiently big (depending on X), one even gets a simple description of T(X) which is uniform in p. In the talk, I will present this description. For arbitrary p (i.e. including small ones), I only have a conjectural description of the trees. This conjecture should also hold for slightly more general X ("semi-algebraic sets over the p-adics"), and in this generalized setting, the "converse" of the conjecture holds: any tree satisfying this description can be obtained as T(X) for a suitable X. Thus the conjecture describes the trees "as precisely as possible".

15h-16h Robert Tijdeman (Leiden)

16h30-17h30 Leo Storme (Gand)

: (33) 3 20 43 68 75

: (32) 9 264 49 00