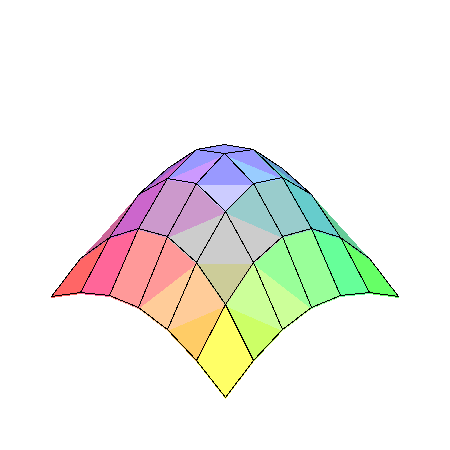Introduction pratique aux EDP

JP Chehab

Méthode des différences finies pour les problèmes stationnaires

( Illustrations Maple du chapitre 4)

On montre ici comment obtenir quelques schémas de base à l'aide Maple .

Construction de schémas à l'aide de la formule de Taylor

La formule de Taylor est le principal outil technique pour construire des schémas aux différences finies. Elle est implentée dans Maple avec la commande taylor .

La formule de Taylor en Maple

On considère, pour simplifier, la discrétisation d'un intervalle par des points régulièrement espacés ; on note h le pas de discrétisation . Soit u une fonction assez régulière. Son développement de Taylor à l'ordre N en x+h au voisinage de h=0 est donné par :

> restart;

> N:=10;

> dev_lim_plus:=taylor(u(x+h),h,N);

On reconnait une formule de Taylor-Young avec la notation de Landau pour le reste. Les dérivées successives sont représentées à l'aide de l'opérateur D .

De la même façon, on peut considérer le dl de u en x-h, au voisinage de 0. On obtient

> dev_lim_moins:=taylor(u(x-h),h,N);

C'est en combinant dev_lim_plus et dev_lim_moins que l'on construit les différents schémas.

Pour plus de simplicité, nous convertissons ces dl en polynômes, à l'aide de la commande convert :

> dl_plus:=convert(dev_lim_plus,polynom);

> dl_moins:=convert(dev_lim_moins,polynom);

Schémas pour les dérivées

Dérivée première

En considérant la différence u(x+h) -u(x), on obtient

> simplify(dl_plus -u(x));

d'où

> schema1:=simplify((dl_plus-u(x))/h);

qui fournit donc un schéma d'approximation de la dérivée première à l'ordre 1 (l'erreur commise est en h).
On appelle ce schéma schéma décentré progressif

De la même manière, on peut considérer la différence u(x)-u(x-h) et, en procédant comme plus haut, on obtient le schéma

> schema2:=simplify((u(x)-dl_moins)/h);

qui est lui aussi d'ordre 1. C'est le schéma décentré régressif

Question : comment déterminer automatiquement l'ordre d'un schéma aux différences avec Maple ?

L'ordre est donné par le degré le plus bas dans la conversion en polynôme du développement limité de la différence entre la différence finie et la quantité à approcher (on se reportera à la définition de l'ordre d'un schéma). Le plus bas dégré d'un polynôme est déterminé à l'aide de la commande ldegree . Par exemple pour schema1 , on a

> ordre:=ldegree(schema1-D(u)(x),h);

et le terme principal de l'erreur est donné par le coefficient de (commande coeff )

> coeff(schema1-D(u)(x),h^ordre)*h^ordre;

En considérant la moyenne arithmétique des schémas 1 et 2 on obtient

> schema3:=simplify(1/2*((u(x+h)-u(x))/h +(u(x)-u(x-h))/h));

c'est aussi une approximation de la dérivée première en x. En effet

> limit(taylor(schema3 -D(u)(x),h,N),h=0);

Calculons son ordre ainsi que le terme principal de l'erreur :

> pschema3:=convert(taylor(schema3,h,N),polynom);

> ordre_schema3:=ldegree(pschema3 -D(u)(x),h);

> terme_principal_erreur_schema3:=coeff(pschema3-D(u)(x),h^ordre_schema3)*h^ordre_schema3;

C'est un schéma centré

Dérivée seconde

En procédant analoguement à ce qui précède, on construit le schéma suivant :

> `u(x+h)+u(x-h)`=convert(dev_lim_plus+dev_lim_moins,polynom);

et donc

> `(u(x+h)+u(x-h)-2*u(x))/h^2`=expand((rhs(%)-2*u(x))/h^2);

ainsi est une approximation d'ordre 2 de .

Interpolation

Il s'agit d'approcher la valeur d'une fonction en un point , connaissant des valeurs de cette fonction en des points lorsque au moins

deux des encadrent . La plus simple situation est la suivante :

Connaissant la valeur (ou une approximation) de u en x+h et en x-h, approcher u(x). En considérant la somme des dl dl_plus et dl_moins, il vient

> dl_plus+dl_moins;

Ainsi

> (dl_plus+dl_moins)/2-u(x);

C'est un schéma d'ordre 2.

Application à la résolution d'EDP elliptiques (en dimensions 1 et 2 d'espace)

Soit I =]0,1[. On considère la discrétisation de I par une suite de N points prédéfinis. On complète cette suite en ajoutant les deux points du bord : et . L'approximation de la solution en les conjointement à la discrétisation des opérateurs différentiels par des schémas aux différences finies, et après prise en compte des conditions aux limites, conduit à un système algébrique de dimension finie. Lorsque le problème considéré est linéaire, le système obtenu l'est également, évidemment, et le cadre mathématique inhérent est l'algèbre linéaire.

Algèbre linéaire et Maple

Le package linalg réunit l'ensemble des commandes Maple en algèbre linéaire.

> restart;

> with(linalg);

Warning, new definition for norm

Warning, new definition for trace

D'un point de vue pratique, pour la résolution numérique "symbolique" d'EDP par différences finies, on se contentera, pour commencer, de savoir

- construire et initialiser un vecteur et une matrice

- résoudre un système linéaire

- déterminer les vecteurs et les valeurs propres d'une matrice

et aussi de savoir

- représenter la solution approchée

Pour avoir quelques exemples d'utilisation de linalg, on pourra également consulter les cours-td-tp de calcul scientifique de licence de mathématiques.

Exemples d'utilisation

Construction d'une matrice

1) Matrice formelle et évaluation d'une matrice i.e. représentation sous forme d'un tableau

> n:=4;

> A:=matrix(n,n);#c'st une matrice formelle n x n

> evalm(A);

2) Lorsque les coefficients doivent être rentrés à la main

Faites donc deux boucles ...

3) Lorsque les coefficients sont connus explicitement en fonction de i et de j. Par exemple, pour la matrice de Hilbert

> coefficients:=(i,j)->1/(i+j-1);

> n:=4;

> A:=matrix(n,n,coefficients);

4) Matrice aléatoire

> randmatrix(n,n);

5) Une matrice "bande", très utile pour les différences finies.

> band([b,a,b],n);

6) Initialisation d'une matrice nulle

> matrix(n,n,0);

Résolution d'un système linéaire

Considérons une matrice aléatoire B de taille n x n

> B:=randmatrix(n,n);

vérifions qu'elle est bien inversible

> det(B);

Choisissons comme second membre le vecteur de taille n avec tous les coefficients égaux à 1.

> F:=vector(n,1);

La solutiondu systeme B*X=F est

> X:=linsolve(B,F);

Vecteurs et valeurs propres

La recherche des valeurs propres est équivalente à la recherche de racines d'un polynôme. A partir de n=5, les choses se gâtent et, sauf miracle, il est recommandé d'avoir recours à des méthodes numériques, se qui se réalise en Maple à l'aide du suffixe 'f' , comme 'float'. On consultera les commandes eigenvals (pour les valeurs propres) et eigenvects (pour les vecteurs propres).

Considérons une matrice aléatoire de taille N

> N:=4;

> C:=randmatrix(N,N);

> allvalues(eigenvals(C)):

si on passe en flotttants

> C1:=map(evalf,C);

> eigenvals(C1);

> eigenvects(C1);

>

Résolution d'un problème de Dirichlet en dimension 1

La résolution des systèmes linéaires sera effectuée ici à l'aide de la commande linsolve , donc avec une "boite noire". On discutera ailleurs des méthodes

d'algèbre linéaire numérique qui devront être employées dès que la taille du système n'est plus petite ; Maple n'est pas en effet adpaté pour des problèmes plus larges et on utilisera avec plus d'efficacité Matlab ou Scilab .

On considère le problème

- , dans ]0,1[

u(0)=u(1)=0

Construction du système

La discrétisation de ce problème par un schéma à trois points sur un maillage régulier génère le système linéaire :

, pour i=1..N, avec =0 et

La matrice sous jacente est une matrice de type "bande"

> restart;

> with(linalg):

Warning, new definition for norm

Warning, new definition for trace

> N:=10;

> h:=1/(N+1);

> A:=band([-1,2,-1],N)/h^2;

Prenons comme second membre

> f:=x->sin(Pi*x)*exp(x);

> F:=[seq(f(i*h),i=1..N)];

qu'on peut représenter en "flottants"

> F1:=map(evalf,F);

Résolution et représentation de la solution

Le vecteur solution est donné par

> X:=linsolve(A,F1);

On le représente graphiquement par

> liste_de_points:=[[0,0],[k*h,X[k]]$k=1..N,[1,0]];

Par des points

> plot(liste_de_points,x=0..1,style=point,color=blue);

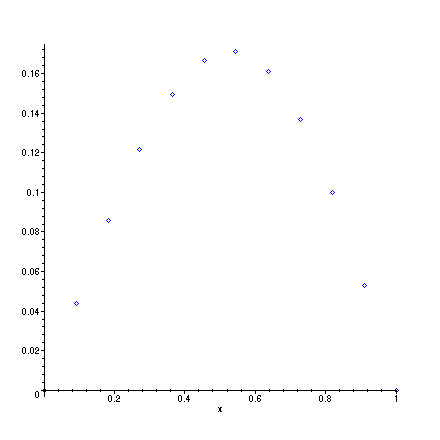
Par un trait continu (fonction affine par morceaux ici )

> plot(liste_de_points,x=0..1);

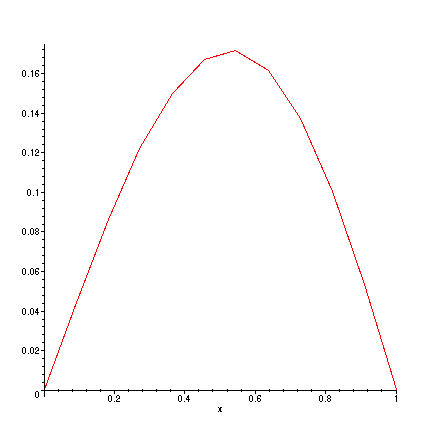
Résolution d'un problème de Dirichlet en dimension 2

Représentation graphique des surfaces avec Maple

On utilise la commande plot3d

N'oubliez pas que vous pouvez modifier le dessin obtenu en utilisant les icônes graphiques qui apparaissent lorsque vous cliquez sur le graphe.

> restart;with(linalg):

Warning, new definition for norm

Warning, new definition for trace

> f:=(x,y)->exp(-16*(x-1/2)^2-16*(y-1/2)^2);

> plot3d(f(x,y),x=0..1,y=0..1);

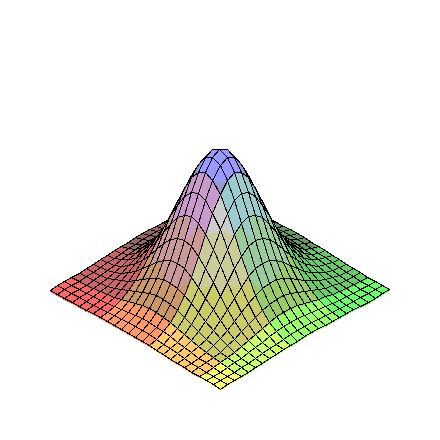
A présent représentons graphiquement une suite de points à double indice. Pour cela il faut représenter cette suite sous forme de matrice et utiliser la commande matrixplot du package plots . Voici ce que cela donne sur notre exemple :

> with(plots):

> N:=10;h:=1/(N+1);

> points:=(i,j)->f(i*h,j*h);

> matrix(N,N,points):

> Mat:=map(evalf,matrix(N,N,points)):

> matrixplot(Mat);

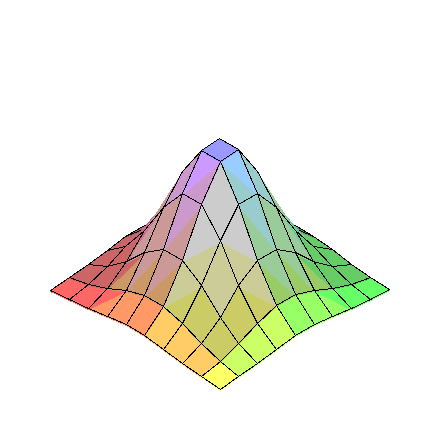
Exercice résolu

On considère le problème de Dirichlet dans le carré unité

dans ]0,1[ x ]0,1[

u(x,y)=0 si x =0 ou 1 ou si y=0 ou 1

1) Constuire une procédure qui, à N donné, construit la matrice de discrétisation de associé à la discrétisation du carré unité avec N points régulièrement espacés dans chaque direction. On notera h, le pas de discrétisation.

2) Résoudre le système produit, pour une "petite" valeur de N (7 par exemple) et représenter graphiquement la solution sous forme de surface ; comme d'habitude le choix de la fonction f vous revient.

Solution

1)

> restart;

> with(linalg):with(plots):

Warning, new definition for norm

Warning, new definition for trace

> lapla_2D:=proc(N)
local A,i,j,k;
A:=matrix(N^2,N^2,0):
for j from 1 to N do
k:=(j-1)*N:
for i from 1 to N do
A[i+k,i+k]:=4;
if i>1 then
A[i+k,i-1+k]:=-1:
fi:
if i < N then
A[i+k,i+1+k]:=-1:
fi:
if j < N then
A[i+k,i+N+k]:=-1:
fi:
if j >1 then
A[i+k,i-N+k]:=-1:
fi:
od;
od;
RETURN(evalm(A));
end:

> lapla_2D(4);

2) On choisit pour second membre la fonction

Construisons le vecteur associé.

> N:=7;

> h:=1/(N+1);

> f:=(x,y)->sin(Pi*x)*sin(Pi*y);

> source:=proc(N,f)
local F,h,i,j,k;
h:=1/(N+1);
F:=vector(N*N,0):
for j from 1 to N do
k:=(j-1)*N:
for i from 1 to N do
F[i+k]:=evalf(f(i*h,j*h));
od;
od;
RETURN(evalm(F));
end:

> F:=source(N,f);

> A:=lapla_2D(N):

> X:=evalm(linsolve(A,F));

Représentons la solution graphiquement. A cette effet réécrivons X comme une matrice N x N

> Mat:=matrix(N,N,0):#initialisation à 0 de la matrice

> for j from 1 to N do
k:=(j-1)*N:
for i from 1 to N do
Mat[i,j]:=X[i+k]:
od:
od:

> matrixplot(Mat);